スペクトラムアナライザを用いて、全高調波歪率(THD)を求めたいと思って、2次、3次、4次、 と高調波を測定しました。
そして、いざ、測定した結果から全高調波歪率を算出しようとした時に、全高調波歪率の定義式から算出しようと考えましたが、けっこう複雑だと感じました。。
面倒くさかった私は、簡単に直ぐ求める方法をネットで検索しましたが、検索結果のほとんどは、理論的な記述をしているだけで、直ぐに結果だけを出したかった私にとっては、役立つ情報ではありませんでした。
そこで、私のように、面倒くさい理屈は抜きにして、結果だけをすぐに求めたい人に役立ててもらおうと、結果だけ直ぐに出す方法を書くことにしました。
余計な理屈が不要な方は、下図(エクセルシートの図)の直前まで読み飛ばして下さい。
全高調波歪とは
全高調波歪率(THD)、いわゆる「ひずみ率」について、簡単に定義だけをいえば、基本波と高調波の実効値の比のことです。
算出する式は、全ての高調波の実効値の二乗の和の平方根を、基本波の実効値で割って100[%]を掛けた値になります。
式で表せば、下記のようになります。
THD(全高調波歪率)= 100 x SQRT{ Σ (En x En)}/E1…(1)
E1:基本波の実効値電圧
En:n次高調波の実効値電圧
SQRT:平方根
問題なのは、通常、スペクトラムアナライザで高調波成分を測定する場合、基本波に対する相対値を測定するので、いちいち実効値を求めたりしません。
従って、上記の定義式を忠実に処理しようとして、わざわざ、基本波や高調波の絶対値を求めて、それらを式に代入するのではとても面倒です。
しかし、全高調波歪率は、比率を求めるだけなので、実際は絶対値を測定する必要はなく、相対値をそのまま計算式に代入してしまえば、それで済むのです。
では、相対値から求める式ですが、下記のようになります。
THD = 100xSQRT{ Σ (10^(Ln/20))^2} = 100xSQRT{ Σ 10^(Ln/10)}…(2)
Ln:n次高調波の相対レベル[dB]
^:べき乗
基本波は基準で0[dB]に相当するので、(1)式における分母は1となって、式から除算部分が無くなるんですね。なので、相対レベル値を(2)式に入れればいいだけです。※
※式(1)から式(2)への置換を詳しく知りたい方は、記事末の補足を参照してください。
実際のエクセル計算式
前置きはここまでにして、まず、(2)式をあらかじめエクセルで作成しておきましょう。
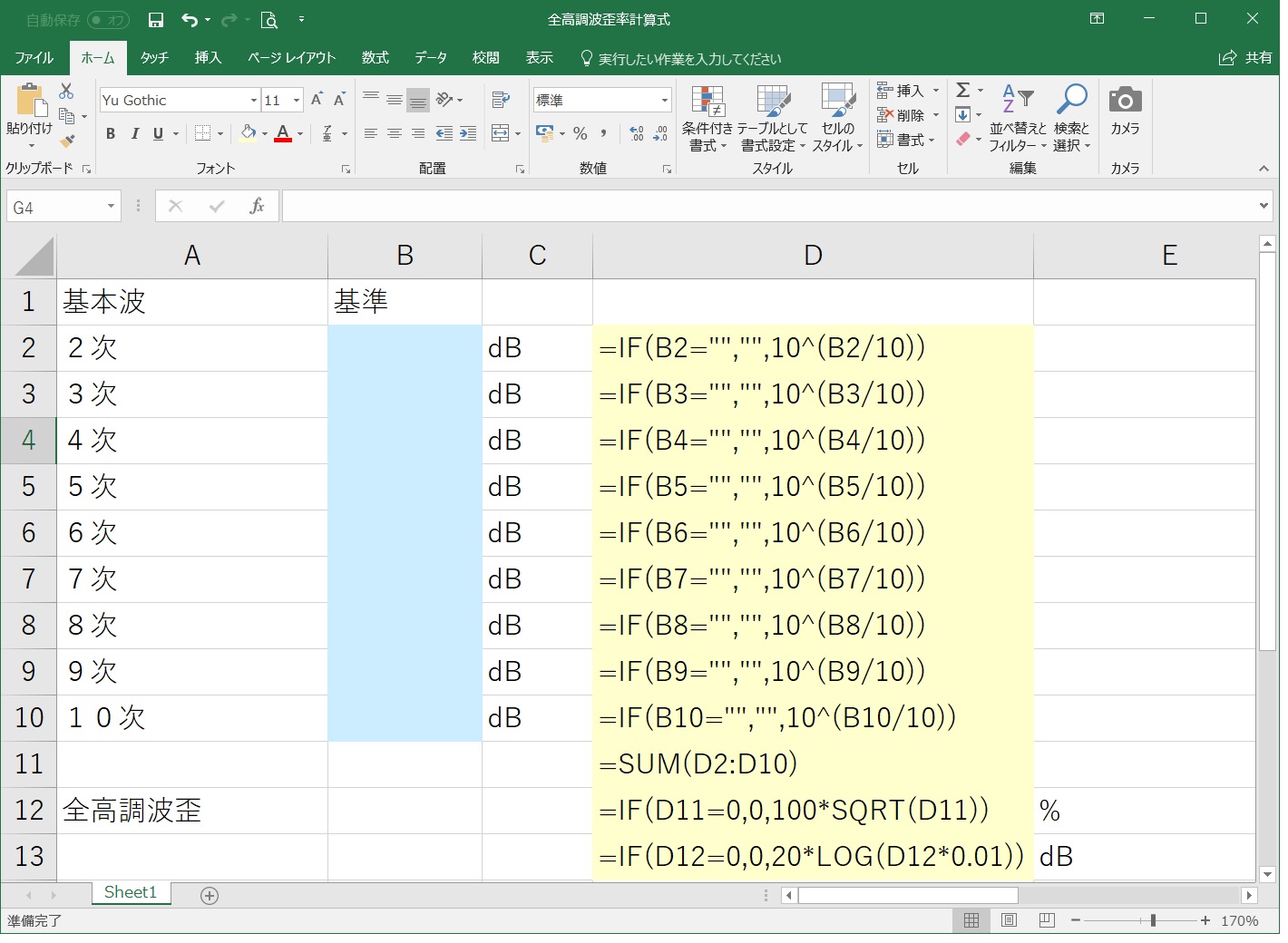
上図のように、黄色部分に計算式を記述しておきます。水色部分が、スペアナで測定した高調波の測定結果(相対値)を入力するセルで、計算結果はセルD12(%表示)とD13(dB表示)に表示されます。
では、実際にスペクトラムアナライザの測定値から求めてみましょう。スペクトラムアナライザの周波数範囲(スパン)を、基本波からその10倍くらいまでに設定して、基本波のレベルを基準に設定します。
そして、二次高調波、三次高調波、 等、高調波の基本波に対する相対値[dB]をマーカなどを利用して読み取ります。
読み取った値は、そのままエクセルシートの水色セルに記入するだけです。
高調波は通常、高次になればなるほどノイズレベルは小さくなり、10次くらいあればあとは無視できるくらい小さくなるので、ここではエクセルの式としては10次高調波までとしました。10次以下の高調波でも、ノイズレベルが十分小さい成分については、空欄で構いません。
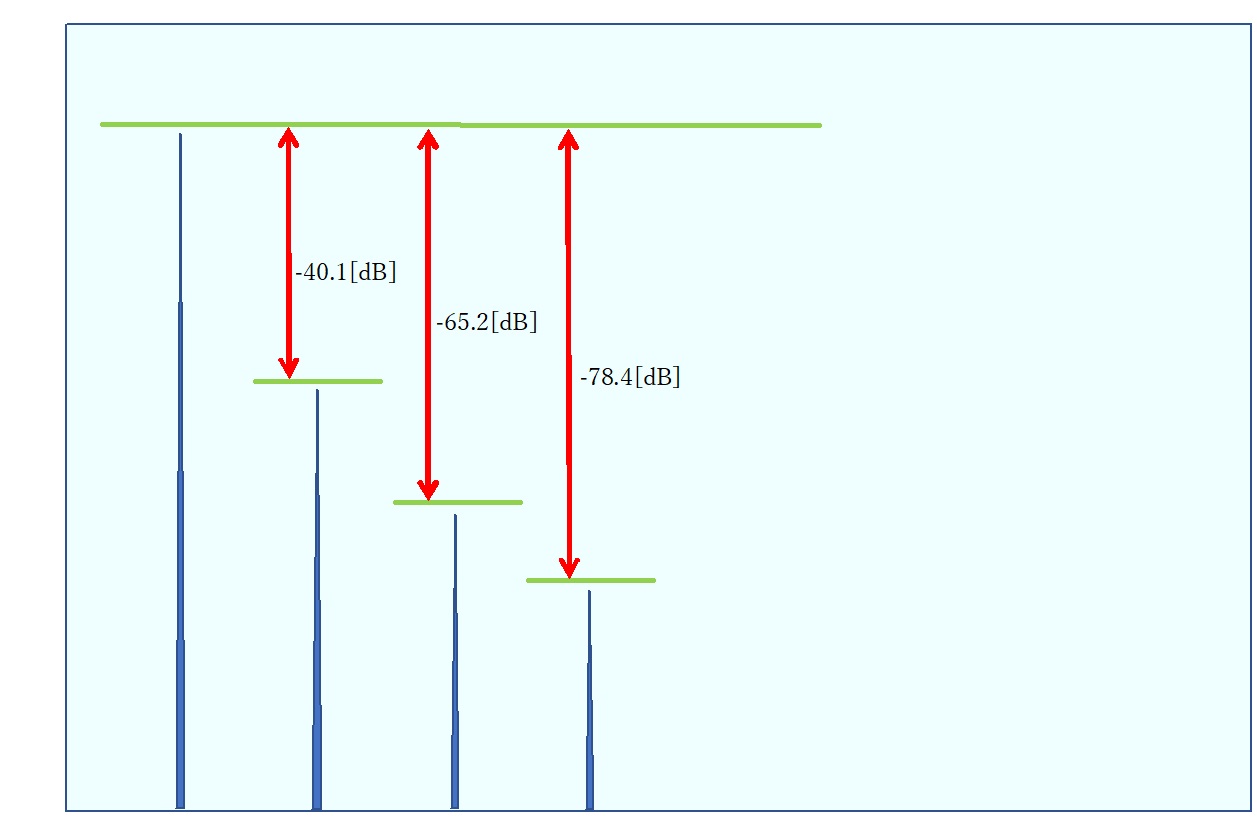
例えば、上図のように測定した値が、-40.1 [dB] (二次高調波)、-65.2[dB] (三次高調波)、-78.4[dB] (四次高調波)だったとして、五次高調波より上は無視できるくらい小さかったとします。
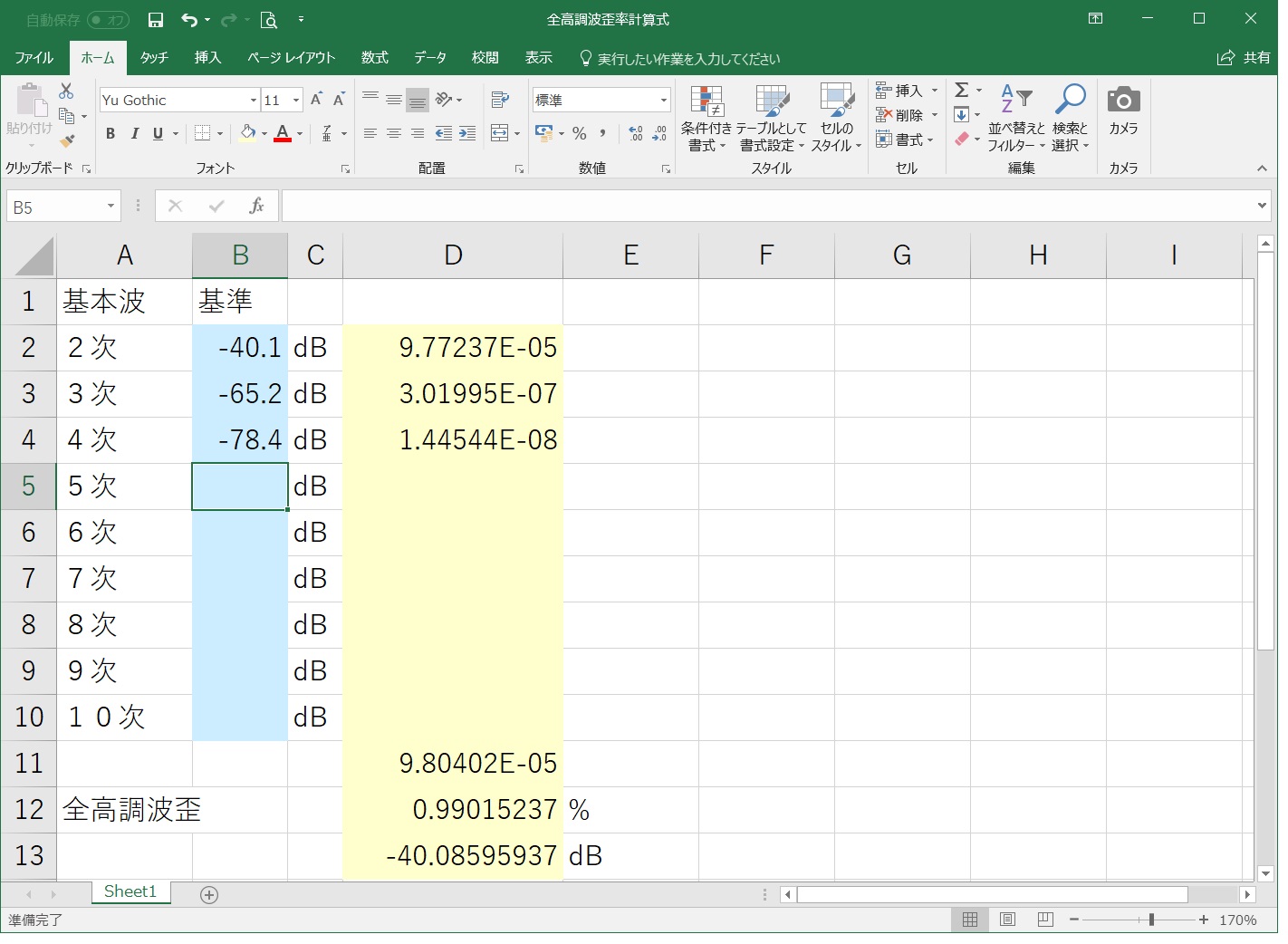
これをエクセルの水色セルに記入すると、結果は0.99[%](-40.086[dB])のようになります。
一度、エクセルで計算式を作っておけば、いつでも使えますので便利ですね。全高調波歪率の算出に役立てて下さい。
なお、信号によっては11次よりも高い高調波を含める必要がある場合もありますが、その場合は上記の計算式に必定な次数分だけ同様に追加して下さい。
補足…式(1)から式(2)への置換に関する詳細説明
では、詳細を知りたい方のために、上記の式(1)から式(2)への置換について補足説明します。
まず初めに、スペクトラムアナライザで読み取る基本波のレベル(絶対値)をP1[dBm]とし、二次高調波をP2[dBm]、三次高調波をP3[dBm]、・・・、n次高調波をPn[dBm]のように表すとします。
そして、高調波成分の基本波に対する相対値をL2[dB](二次高調波)、L3[dB](三次高調波)、・・・、Ln[dB](n次高調波)のように表すと、
L2 = P2 – P1[dB]…(3)
L3 = P3 – P1[dB]…(4)
Ln = Pn – P1[dB]…(5)
のように表せます。
ここで、P1、P2、P3、・・・、Pnにおけるそれぞれの電圧を求めると、その定義(0[dBm]=1[mW])から
E1=SQRT{(Zx10^(P1/10))/1000}[V]…(6)
E2=SQRT{(Zx10^(P2/10))/1000}[V]…(7)
E3=SQRT{(Zx10^(P3/10))/1000}[V]…(8)
En=SQRT{(Zx10^(Pn/10))/1000}[V]…(9)
Z:インピーダンス[Ω]
のようになります。
ここで、式(6)~(9)について、それぞれを二乗して整理すると、
E1^2=(Z/1000)x10^(P1/10)…(6)’
E2^2=(Z/1000)x10^(P2/10)…(7)’
E3^2=(Z/1000)x10^(P3/10)…(8)’
En^2=(Z/1000)x10^(Pn/10)…(9)’
のようになります。
全高調波歪率THDは、前述のように
THD= 100 x SQRT{ Σ (En x En)}/E1…(1)
でした。今、この式(1)を変形すると、
THD= 100x(E2^2 + E3^2 +・・・+En^2)^(1/2)/E1…(10)
更に、
THD= 100x(E2^2 + E3^2 +・・・+En^2)^(1/2)/(E1^2)^(1/2)…(11)
のようになりますから、分母と分子をまとめると、
THD= 100x{(E2^2 + E3^2 +・・・+En^2)/E1^2}^(1/2)…(12)
のようになります。
今ここで、式(12)に式(6)’~式(9)’を代入します。
式(6)’~式(9)’中の”(Z/1000)”は、全ての式で共通なので、式(12)中の分母と分子で打消し合った結果、式(12)は下記のようになります。
THD= 100x{(10^(P2/10) + 10^(P3/10) +・・・+10^(Pn/10))/10^(P1/10)}^(1/2)…(13)
この式を、分子の各項ごとに分母で割る記述に変形すると、
THD= 100x{10^(P2/10)/10^(P1/10) + 10^(P3/10)/10^(P1/10) +・・・+10^(Pn/10)/10^(P1/10)}^(1/2)…(14)
のようになります。
今、10^(P2/10)/10^(P1/10)=10^{(P2-P1)/10}が成り立ちますから、式(14)は、
THD= 100x〔10^{(P2-P1)/10} + 10^{(P3-P1)/10} +・・・+10^{(Pn-P1)/10}〕^(1/2)…(15)
のようになります。式(15)に式(3)~(5)を代入すると、
THD= 100x {10^(L2/10) + 10^(L3/10) + ・・・+10^(Ln/10)}^(1/2)…(16)
のようになります。これは、上記に示した
THD= 100xSQRT{ Σ 10^(Ln/10)}…(2)
を意味しますので、式(1)を式(2)に置き換えられることが分かります。

