ワードで作成する文書中に表を書くことがありますが、ワードの表でもエクセルのように表計算ができます。
表にはエクセルを使うのが一般的ですが、文書の性質上、ワードが望ましい場合にはともて便利です。
私も、以前はこの機能を知らず、わざわざエクセルで計算してから、ワードで作表していました。
ワードの表計算機能を知らないと、たとえ小さな表を作る場合でも、とても煩わしいので、覚えておきたいものです。
以下、ワードの表における、表計算の仕方を説明します。
目次
基本的な手順
まず、ワード中に表が書かれているものとして、表の中で、計算式を記述したいマス目(セル)にカーソルを持って行きます。(下図)
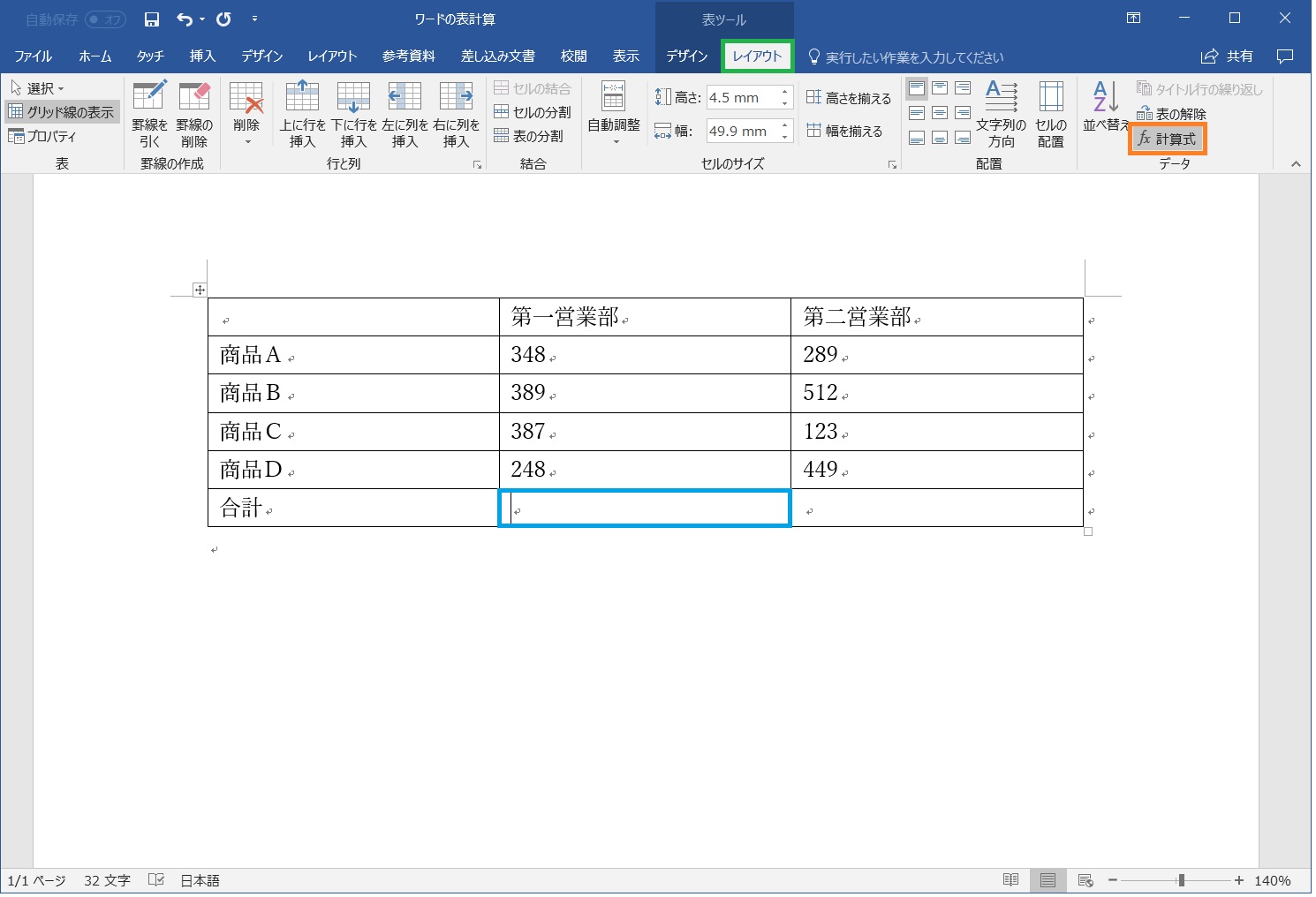
計算式を記述したい表
すると、リボン上にレイアウトタブが現れるので、これをクリックします。(このタブは、表または、表中のマス目を選択しないと現れません)
クリックするとリボンのデータグループ内に「fx 計算式」というコマンドが表示されますので、これをクリックします。
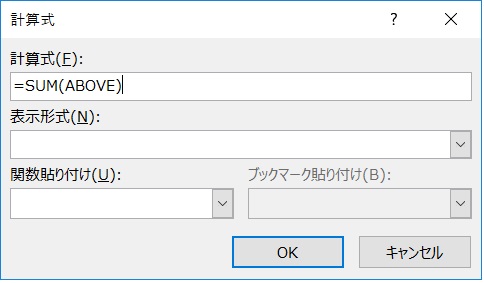
計算式記述用のダイアログボックス
クリックすると、計算式を記述するための「計算式」ダイアログボックス(上図)が現れます。
このダイアログボックス中の計算式欄には、候補の計算式(ここでは「=SUM(ABOVE)」)が表示されますので、内容を確認してOKをクリックします。
ここで、他の関数を選びたい場合は、関数貼り付け欄から選んで記述します。
計算対象となるマス目は通常、ABOVEやLEFT等(場所引数と呼称)を使って表中の位置を記述します。
この例では、ABOVEなので、計算式を記述するマス目より上の、すべてのマス目が対象となります。
つまり、計算式より上(ABOVE)にあるマス目の数値を全て足す(SUM)ことになります。
表示形式は、エクセルでユーザー定義する場合と同じ書式で記述しますが、ここでは空欄(ディフォルト設定)としておきます。(詳細は、後述)
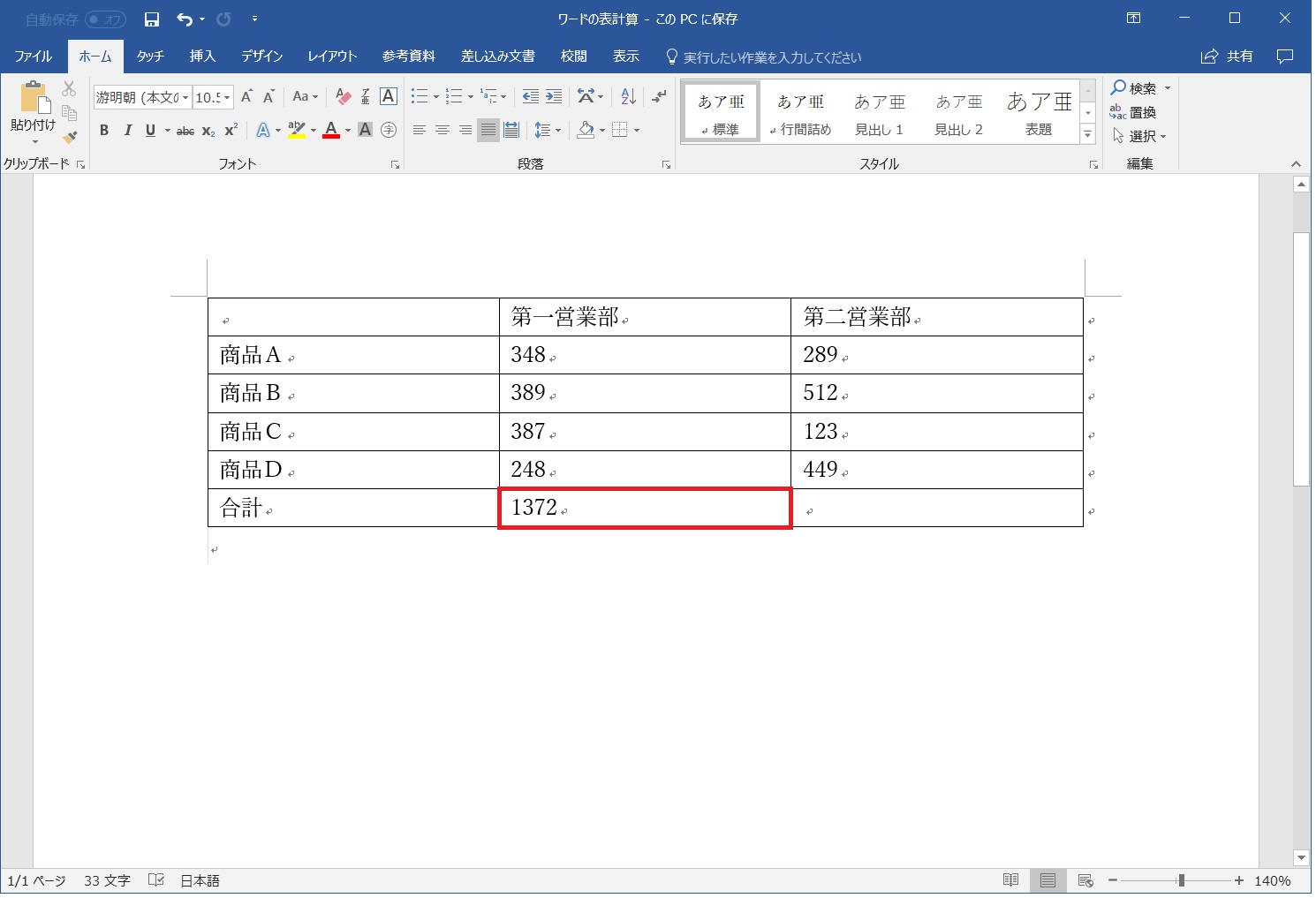
計算結果が自動で表示される
OKをクリックすると元のワードの画面に戻りますが、計算結果が表中に反映されているのが分かります。
なお、ABOVEなど場所引数と呼ばれる引数を用いる場合、見出しの行や列(上記の例では「第一営業部」)は計算対象に含まれません。
ワードの表計算で注意すべきこと
ワードの表計算を利用する場合に、特に注意しなければならないことが2点あります。(下記)
- 数値変更後は必ず更新する
- 場所引数を使う場合はセルを空欄にしない
・数値変更後は必ず更新する
ワードの表計算では、計算式を記述した後で計算される数値を変更した場合、計算結果が自動で更新されません。
従って、計算に用いる数値を変更した場合は、必ず更新処理をする必要があります。
具体例を挙げましょう。
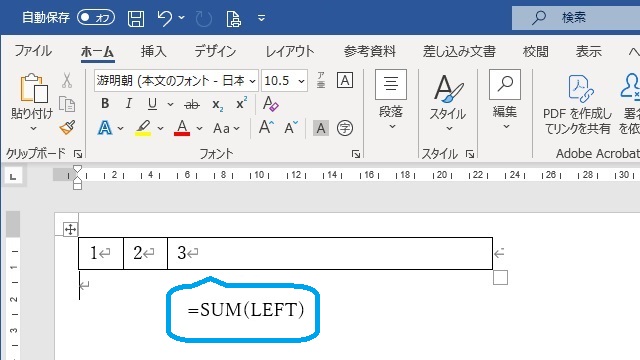
1+2をSUM関数で計算している
上記の例では、SUM関数を使用して1+2を計算させ、結果3が表示されています。
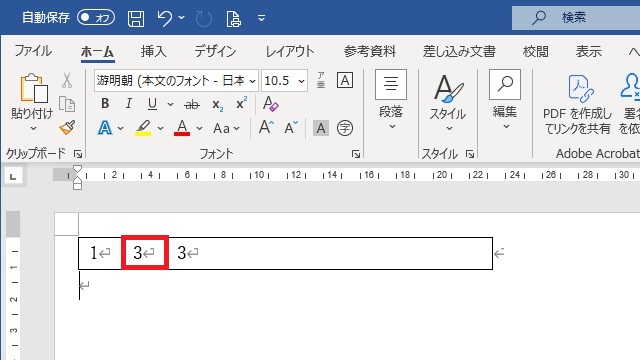
計算される数値を変更しても計算結果に反映されない
この時、計算される数値のうち「2」→「3」を変更しても、結果は元の「3」のまま変わりません。
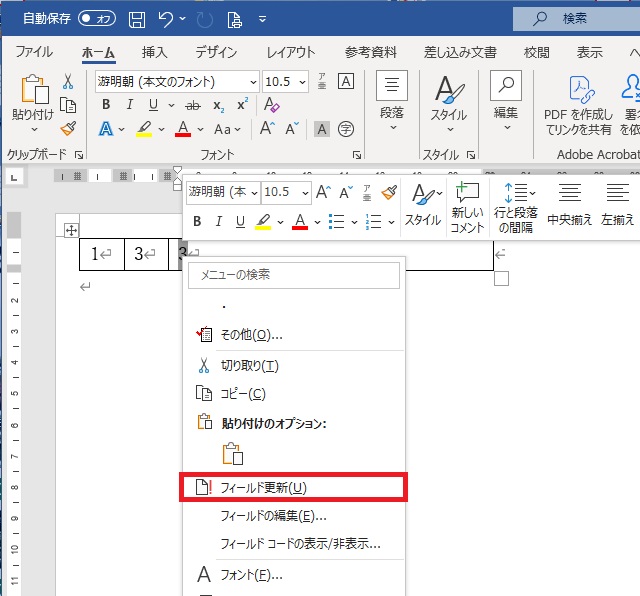
手動で更新する必要がある
この場、更新したい計算式をカーソルで選択して、右クリックから「フィールドの更新」を選択する操作が必要です。
ここで、計算式を含むセル(マス目)の選択ではなく、計算式に相当する数値を選択する必要がありますので間違えないよう注意して下さい。
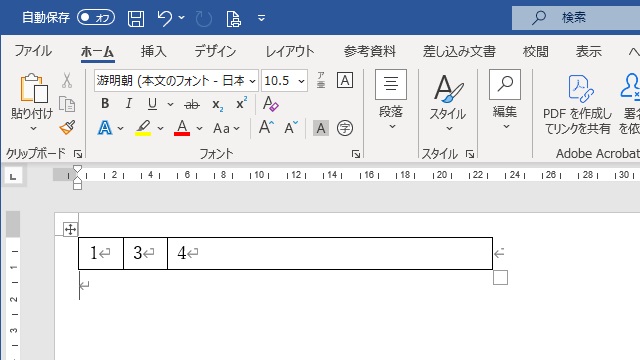
更新すると正しい値になる
「フィールドの更新」後は、上記のように正しい値「4」になることが分かります。
表中で複数の計算式を記述している場合、一度の操作で全ての表を更新することができます。
下記の例は、各行の最終列に「=SUM(LEFT)」と記載されていますが、数値を変更したため、いずれも計算結果が正しい値になっていません。
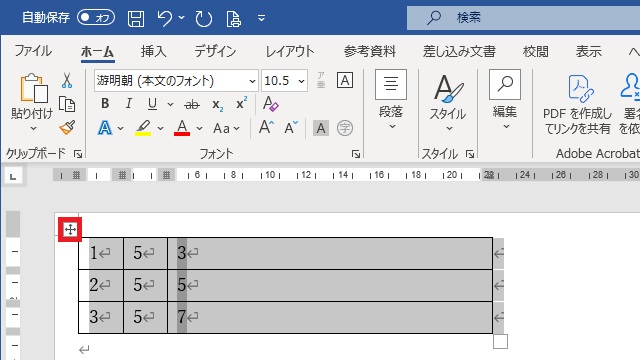
いずれも計算結果が正しくないので、+マークで表を選択してF9キーで更新させる。
表中の全ての計算式を更新する場合は、表の左上にある「+」マークをクリックして表全体を選択後、ファンクションキー「F9」を押します。
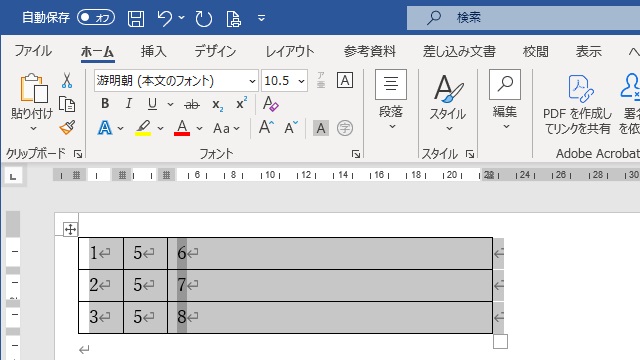
更新されて、正しい結果が表示される
すると、表中の計算式が全て更新され、正しい結果が反映されます。
なお、ワード文章中の全ての計算式を更新したい場合は、
「Ctrl」+「A」(コントロールキーを押しながらAキーを押す)
で、文書全体を選択した後、ファンクションキー「F9」を押せば、処理できます。
・場所引数を使う場合はセルを空欄にしない
ワードの表計算における、もう1つの注意点は、場所引数(LEFT、RIGHT、ABOVE、BELOW)を使う場合は、セルを空欄にしないことです。
これは、誤動作を防止する上で重要です。
分かりやすい例を挙げてみます。
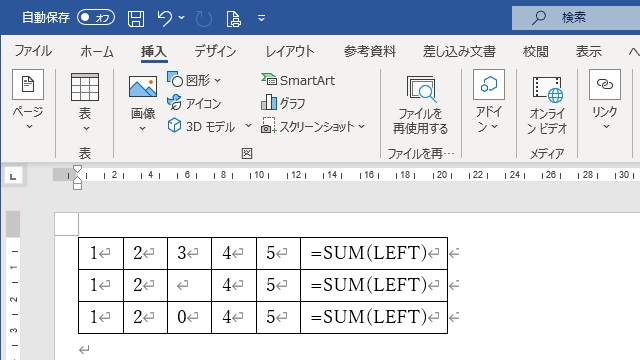
空欄がある場合の例
この例では、1行目で1,2,3,4,5の合計をSUM関数で計算させています。
2行目では、上記のうち「3」を含んでいたセルを空欄に変えます。
同様に、3行目では「3」を含んでいたセルを「0」に変えます。
では、計算式の結果はどのようになるか見てみましょう。
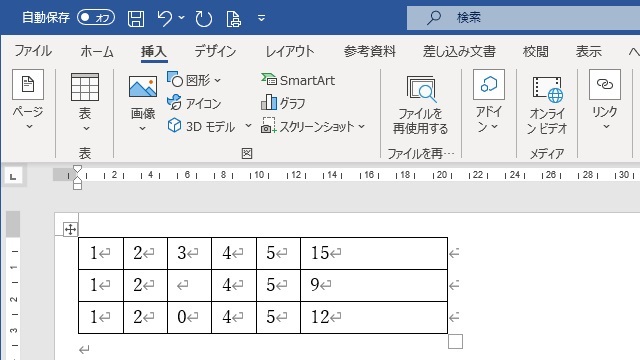
空欄があると意図しない動作になる
「あれっ?」
と思った方も多いと思います。
1+2+3+4+5=15(1行目)ですから、3を除いた結果(2行目)は「12」になると考えるのが自然です。
ところが、2行目の結果は「9」となっています。(3行目は「12」になっている)
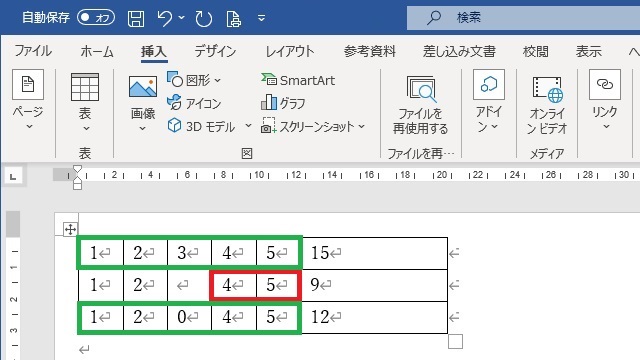
空欄がある場合の計算(参照)対象
計算対象となっているセルを示すと、それぞれ上記の色枠(赤や緑)です。
2行目の例では、赤枠に示すように全てのセルが対象となっていません。
この理由は、場所関数を使用する場合、場所を示す方向のセルは全て数値である必要があるからです。
数値でない空欄は数値と判断されないため、それより左(場所関数LEFTの場合)にあるセルの数値「1」や「2」は無視されてしまうのです。
場所関数を使用する場合、対象が0(ゼロ)でも空欄にはせず、三行目のように必ず0(ゼロ)を記入することが大切です。
関数は限定されるが工夫次第で幅広く利用できる
さて、ワードの場合は、エクセルと異なり、使える関数は限られています。(下記)
ワードで使える関数ABS, AND, AVERAGE, COUNT, DEFINED, FALSE, IF, INT, MAX, MIN, MOD, NOT, OR, PRODUCT, ROUND, SIGN, SUM, TRUE
また、基本的にABOVE等を使って参照対象のマス目(セル)の指定するものです。
だから、ちょっと複雑な計算はできないように思われます。
しかし、エクセルと同じように四則演算子等が利用できますし、参照をセル番号で記述できるので、けっこう自由度の高い記述が可能です。
ワードの表中の位置を表す番号は、下記のようにエクセルと同じで、行が1,2,3等の数字、列がA,B,C等のローマ字になります。
| A 1 | B 1 | C 1 | D 1 |
| A 2 | B 2 | C 2 | D 2 |
| A 3 | B 3 | C 3 | D 3 |
| A 4 | B 4 | C 4 | D 4 |
| A 5 | B 5 | C 5 | D 5 |
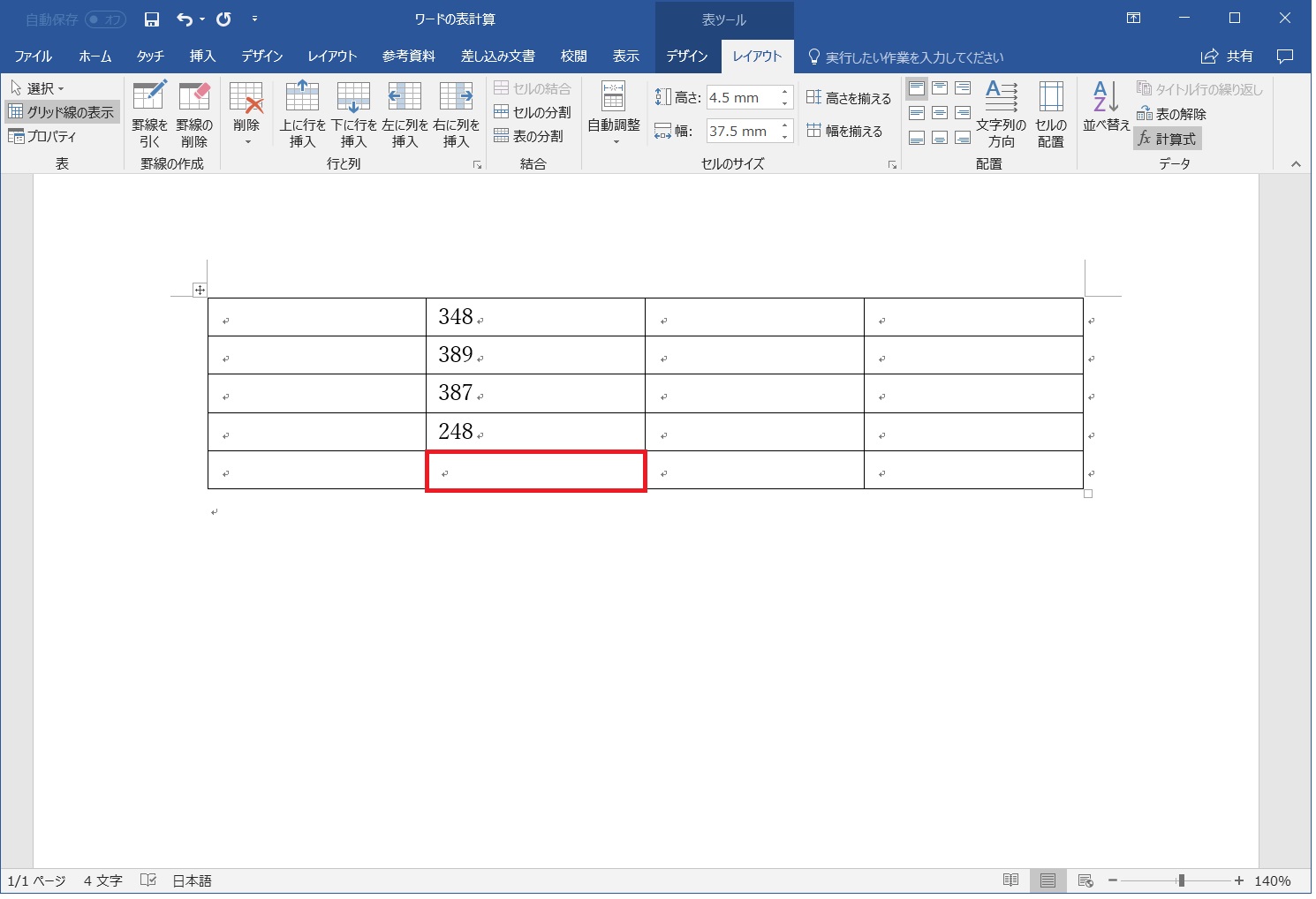
下の図を見て下さい。赤で囲ったB5に相当するマス目に、B1からB4に関する計算式を記述することにしましょう。
赤で囲ったマス目にカーソルをあて、同様に「レイアウト」-「データ」-「fx 計算式」をクリックします。
エクセルのセルに見立てる
前と同様に「計算式」ウィンドウが開くので、計算式欄に、例えば「=B1+B2+B3+B4」のように記述します。(下図)
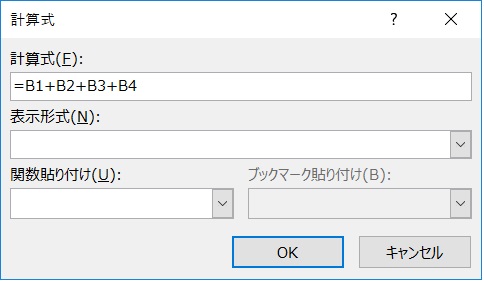
エクセルのように記述
「OK」をクリックして元の画面に戻ります。
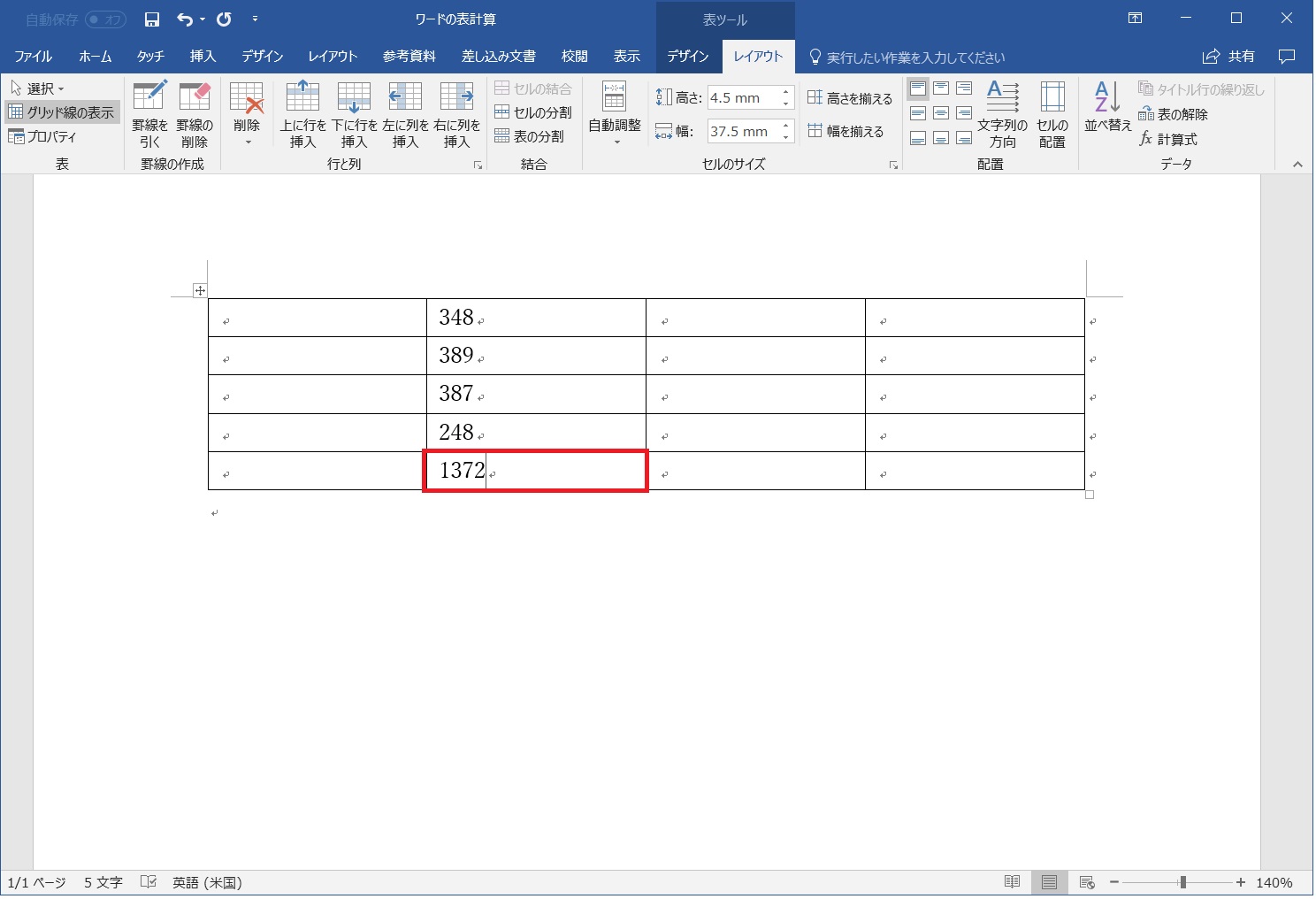
計算結果が反映された
図のように、計算結果が反映されているのが分かります。
このように、ワードにおける表でも、エクセルと同じように表計算ができます。
そして、「計算式」ウィンドウの表示形式欄で所望の形式を指定すれば、表示形式も指定できます。
使い方しだいでは、いろいろな使い方ができますので、うまく利用してみてはいかがでしょう。
なお、ワードの表にはエクセルのようにA1、B2、C3のようなセル番号がありませんので、大きな表を作成する場合などは、表外にA1等の目印を暫定的に記述しておくと扱いやすくなります。
用途別の具体例
基本的な使い方は上記に説明した通りですが、関数は限定され、使用上の制約もありますので、以下、分かりやすいように用途に合わせた具体例を挙げておきます。
加算、足し算、合算、合計、累計、集計
ワードの表計算の場合、加算や合計などには、「SUM関数」や「+演算子」を使います。

足し算にはSUM関数や+演算子を使う
上記の例では、白色セルの数値を加算、合計した結果を薄オレンジのセルに示しています。
表の右側にある別表には、実際に記述していある計算式を示しています。
通常、合計(集計、合算)するには①のようにSUM関数を利用するのが便利です。
場所引数「LEFT」を使用することで、計算式の左にある同じ行内の数値を全て足し合わせることができます。(同様に、「RIGHT」を使えば右にある同じ行内の数値を、「ABOVE」を使えば上にある同じ列内の数値を、「BELOW」を使えば下にある同じ列内の数値の加算が可能)
また、②のように場所関数を使わず、エクセルと同様の参照範囲の記述もできます。
参照範囲が同じなので、計算結果は①と同じになっています。
更に、③のように参照範囲を限定すれば、限定した範囲を足し合わせてくれます。
この方法は、④のようにセルとセルの間が離れている場合でも可能です。
そして、SUM関数の代わりに「+演算子」を用いた計算もできます。
⑤は、「+演算子」を用いて足し算を記述した例ですが、記述方法はエクセルと同様です。
⑥のように、足し合わせる対象のセルを個々に指定することも可能です。
なお、エクセルで使用できるadd関数や、subtotal関数は、ワードの表計算では使うことができません。
引き算、減算、差分
ワードの表計算の場合、引き算などには、「-演算子」を使います。
引き算には-演算子を使う
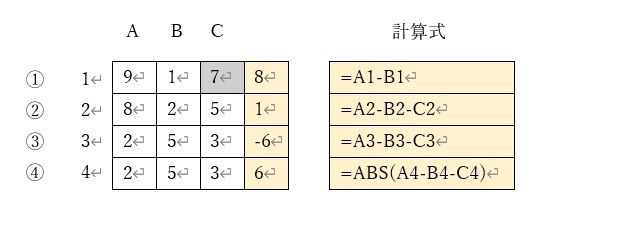
上の例では、左側の表の薄オレンジのセルに、右側の表の薄オレンジに示した計算式が記述されています。
参照範囲は、エクセルで指定する時と同様のセルの番号を用います。
①は、セルA1の値からセルB1の値を引く最も一般的な方法です。(例では、セルC1は参照対象外)
②は、引く数が複数ある場合の例です。
③も②と同じく、引く数が複数ある場合ですが、計算結果が負(マイナス)となる例です。
④は、③と同じような計算をさせていますが、ABS関数を併用することで、差分の絶対値を求めています。
なお、エクセルと同じくワードの表計算には引き算専用の関数はありません。
掛け算、乗算
ワードの表計算の場合、掛け算や乗算には、エクセルでも使う「PRODUCT関数」や「*演算子」を使います。
掛け算にはPRODUCT関数や*演算子を使う
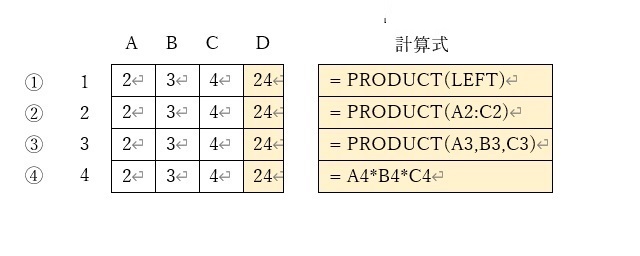
上図では、左側の表の薄オレンジのセルに、右側の表の薄オレンジに示した式が記述されています。
①のように、掛け算では、PRODCUT関数を用いるのが一般的です。
①では、左にあるセル(A1,B1,C1)を全て掛けることを意味しますので、2x3x4=24という結果になります。
②では、場所関数を用いず、エクセルと同じような参照範囲の記述をしています。
③も②と同様、エクセルと同じような記述ですが、参照範囲を別な方法にしています。
④は、PRODUCT関数を用いず、「*演算子」を使っています。
このような記述では、乗算する対象のセルを1つ1つ細かく指定することができます。
なお、エクセルで使える積に関連する関数SUMPRODUCTやDPRODUCTなどはワードでは利用できません。
但し、SUMPRODUCTの場合、「=A1*B1+C1*D1」のように四則演算の記号を併用すれば、同じ計算を行うことはできます。
割り算、除算、剰余、余り、割合、率、パーセンテージ
割り算では、割り切れないケースも多いため、表示桁数が重要になる場合があります。
この場合、既に説明したダイアログボックス中の表示形式(下図参照)の記述がポイントです。

計算式記述用のダイアログボックス
ワードの表で割り算をする場合は、計算式に「/演算子」を用います。
割り算には/演算子を使う
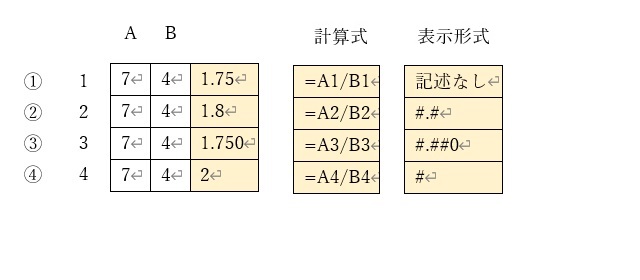
上図では、左側の表の薄オレンジのセルに、中央の表の薄オレンジに計算式を、右側の表の薄オレンジに表示形式を示しています。(表示形式は、計算式記述用のダイアログボックスの中央に記述欄があります)
①のように、割り算には「/演算子」を用います。表示形式を特に指定していないのでデフォルトの桁数で表示されます。
②の場合、計算式は①と同じですが、表示形式を「#.#」としていますので、小数点以下1桁に丸められた(四捨五入)値になっています。
③では、表示形式を「#.##0」としていますので、小数点以下3桁の表示になっています。小数点以下二桁までで割り切れる数ですが、3桁を指定しているため、小数点以下の3桁目が「0」と表示されます。
④では、表示形式を「#」としていますので、小数点以下の表示がない整数だけの表示になっています。
これらを見て分かるように、割り算では表示形式の指定が重要ですので、表示形式には気を付けましょう。(表示形式の記述の仕方はエクセルとほとんど同じです。)
以上のように、一般の割り算は、分数でも表現できますので、上記のように「/演算子」を用います。
しかし、割り算の中には、商を整数で表し、余りを求める場合もあります。
小学校の文章題の問題で、「リンゴガ7個あります。4人で分けるとひとり幾つずつで、何個余りますか?」のような場合です。
そのような場合には、エクセルでもサポートしているINT関数(小数を切り捨てて整数を返す)やMOD関数(余りを計算)を利用できます。
割り算で、商を整数で表して、余りを求める場合、下記のような計算式にします。
整数の商と余りを求める場合はINT関数とMOD関数を使う
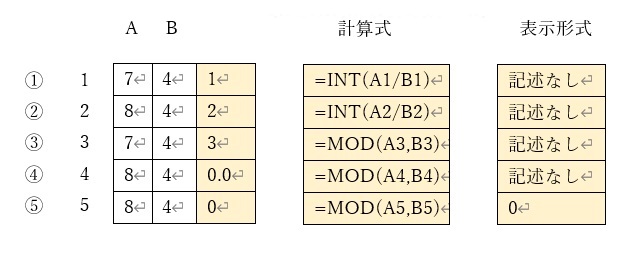
上図では、左側の表の薄オレンジのセルに計算結果を、中央の表の薄オレンジには計算式を、右側の薄オレンジには表示形式を記述しています。
ここでは、下記の2つの式の計算をしています。
7÷4=1・・・(余り)3(例①③)
8÷4=2・・・(余り)0(例②④⑤)
①②はINT関数を利用して商を求め、③④⑤はMOD関数を利用して余りを求めています。
①では、「/演算子」で割り算した結果をINT関数(ワードでもサポート)を用いて処理しています。
①を見て分かるように、7÷4の結果が1になっています。
同じ計算式の②でも、8÷4の結果が2となっていて、きちんと計算されていることが分かります。
余りを求める③の場合、計算式も引数の記述もエクセルのMOD関数と同じです。
余り3がきちんと求められていることが分かります。
一方、余りを求める④の場合、計算式も引数の記述もエクセルのMODと同じですが、結果が「0.0」となっています。
これは、ワードの表計算では、余りが無い場合に、「0」ではなく「0.0」を返すからです。
従って、ワードの表計算で余りを求める場合には、MOD関数を使うと同時に、⑤のように表示形式に「0」を記述しておく必要があります。
さて、割り算と言えば、割合や率、パーセンテージ(百分率)などと密接に関わります。
パーセントなどを表現する具体例を見てみましょう。
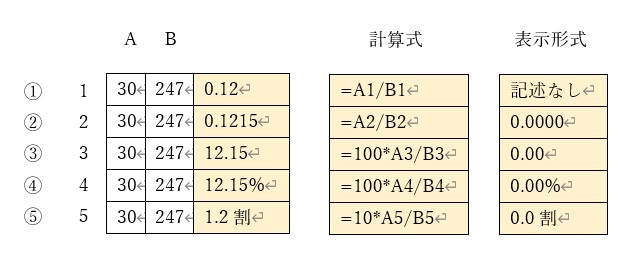
割合等を計算する場合は表示形式が重要になる
①のように、単純な割り算を行えば、割合を計算することができます。
②のように、表示形式で桁数を指定すれば、割合の表示桁数を調節することもできます。
③のように、割り算の結果と100を掛ければ、パーセンテージ(百分率)を計算することができます。
また、④のように、③の表示形式に「%」をつけ加えると、パーセントを含めた表記も可能です。
④のように、計算結果に何らかの文字列(ここでは「%」)を併記させる場合、エクセルの表示形式とは異なりますので注意が必要です。
エクセルの場合、表示形式は「0.00%」ではなく「0.00″%”」のように「”」(ダブルクオーテーション)で囲む必要がありますが、ワードでは不要です。(付けてはいけません)
ちなみに、⑤のように割り算の結果に10を掛ければ、「何割」であるかを表記することもできます。
平均値、アベレージ、最大値、最小値
平均値、最小値、最大値などの基本的な統計計算は、ワードの表でも可能です。
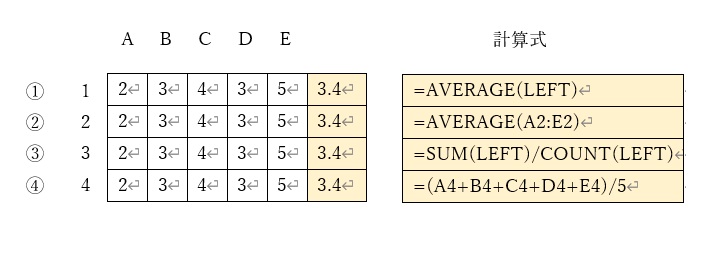
基本的な統計計算ならワードでもできる
まず、平均値(アベレージ)についてですが、①のようにAVERAGE関数を利用します。
この関数は、LEFTなどの場所引数の利用が可能ですので、①のような計算式にするのが自然です。
②のように、参照先を場所引数を使わない方法も可能です。
③のように、SUM関数(合計)とCOUNT関数(カウント)及び「/演算子」を組み合わせても実現できます。
SUM関数もCOUNT関数も共に場所引数が使えるので、記述としては割とシンプルです。
また、④のように、「+演算子」と「/演算子」を組み合わせて実現することも可能です。
③、④は計算式が複雑になりがちですので、特段の理由がない限り、AVERAGE関数を使う方がいいでしょう。
次に、最大値、最小値の場合です。
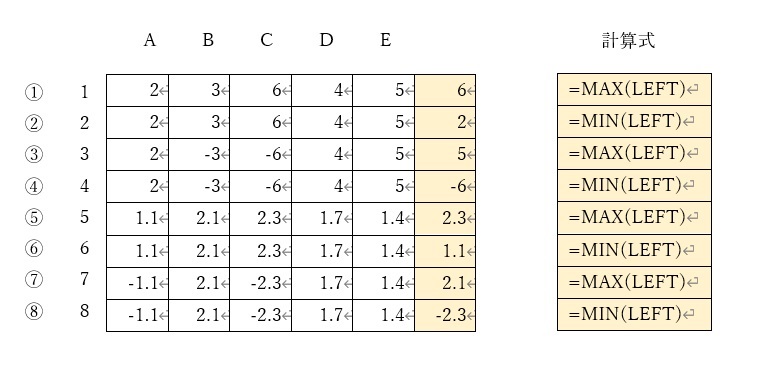
最大値、最小値にはMAX関数、MIN関数を使う
①のように、最大値はMAX関数を利用できます。引数には、LEFTなどの場所引数が使えます。
同様に、②のように最小値にはMIN関数を利用できます。①と同じく場所引数が使えます。
①では最大値「6」が、②では最小値「2」がきちんと求められていることが分かります。
MAX関数もMIN関数も、場所引数ではなく、A1、B2などを用いて参照先を指定することもできます。
③④は、MAX,MINそれぞれの関数を用いた負の数を含めた場合の例です。
正負(プラス、マイナス)を含めて、最大値、最小値が求められていることが分かります。
⑤⑥は、MAX,MINそれぞれの関数を用いた小数を含めた場合の結果です。
小数の場合も、きちんと最大値、最小値が求められていることが分かります。
⑦⑧は、MAX,MINそれぞれの関数を用いた負の小数を含めた場合の結果です。
正負(プラス、マイナス)を含んだ小数でも、最大値、最小値が正確に求められていることが分かります。
このように、ワードの表計算では、平均値、最小値、最大値などの基本的な統計計算が簡単に実現できます。
四捨五入、切り上げ、切り捨て、まるめ
ワードで四捨五入をする場合は、ROUND関数を使います。
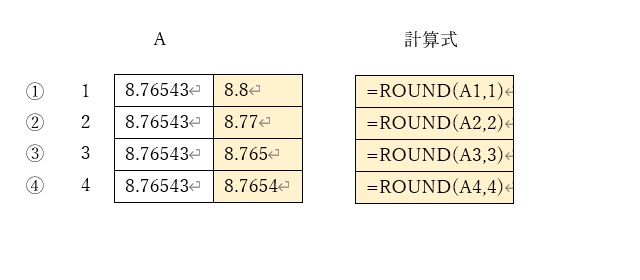
四捨五入にはROUND関数を使う
ROUND関数の使い方は、エクセルのROUND関数と基本的に同じで、四捨五入の処理がされます。
1つ目の引数にまるめる対象を記述し、2つ目の引数で小数点以下何桁にまるめるかの桁数を指定します。
①では、2つ目の引数で「1」を指定していますので、小数点以下1桁にまるめられています。
小数点以下2桁目(=「6」)が四捨五入されて繰り上げられ、8.8になっています。
②では、小数点以下2桁にまるめるため、小数点以下3桁目の「5」が四捨五入されて繰り上げられ、8.77になっています。
以下、同様に③では小数点以下3桁へのまるめ、④では小数点以下4桁へのまるめがされています。
いずれも、エクセルのROUND関数と同様であることが分かります。
ちなみに、①~④は表示形式を指定していませんので、ディフォルトの桁数まで表示されますが、表示形式で桁数を別に指定すれば、有効桁数と表示桁数を別々に管理できます。
例えば、①の表示形式を「#.000」のようにすれば、結果は「8.8」ではなく「8.800」となります。
以上、説明してきたように、四捨五入には、ROUND関数がとても役立ちます。
次に、切り上げや切り捨てについて説明します。
エクセルの場合、ROUNDUP関数やROUNDDOWN関数がありますので、切り上げや切る捨てはこれらの関数を利用して容易に実現できます。
しかし、ワードの表では、ROUNDUP関数やROUNDDOWN関数が使えませんので、工夫が必要です。
では、切り上げの場合の記述例を先に示します。
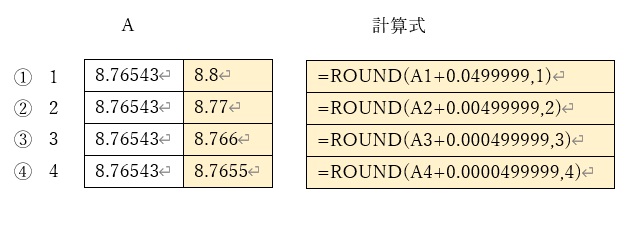
切り上げは、ROUND関数を工夫して使う
①では、小数点以下二桁を切り上げて、小数点以下一桁の数字にしています。
まるめ処理を行う「A1」に予め「0.049999」を足し合わせてから、ROUND関数でまるめ(四捨五入)ています。
これにより、元の数値「A1」を切り上げた結果が反映されます。
切り上げる桁(小数点以下2桁目)に5未満の最大値(ここでは、0.0499999)を加えることで、ROUND関数による処理が事実上、切り上げになります。
四捨五入なので、「0.05」を加えればよさそうに思えますが、元の数値がキリのよい数字(小数点二桁以下が全てゼロ)の場合には、正確に処理されなくなります。
例えば、元の数値が「1.10」の場合、小数点以下2桁目を切り上げても「1.1」のままですが、もし「0.05」を加えてしまうと、「1.15」を四捨五入することになるので「1.2」になってしまいます。
つまり、「1.10」の切り上げは「1.10」のままであるべきところ、「1.20」となり、正常に処理されないのです。
このことから、「5」ではなく「5未満の最大値」を加える必要があるのです。
ちなみに、「0.049999」ではなく「0.049」でも十分ではないかと感じますが、幾つかの計算を繰り返した後にまるめ処理を行う場合などでは、計算誤差が蓄積して悪影響を及ぼす可能性がありますので、「9」を多めに付けておいた方が確実です。
②③④は、まるめる桁数を変えた場合を示していますが、考え方は①と同様です。
いずれも意図する結果になっていることが分かると思います。
では、もう少し詳しく見てみましょう。
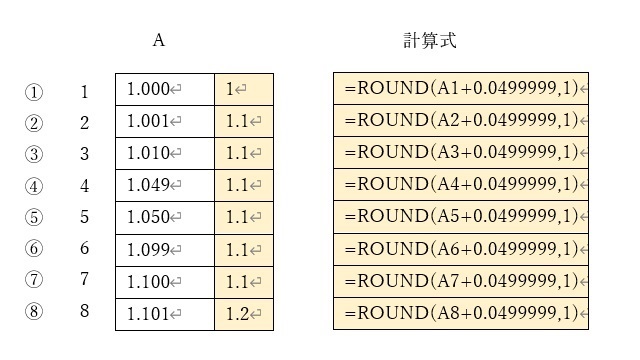
上の図では、小数点以下二桁目を切り上げて、小数点以下1桁にまるめています。
①は、元の数値が「1.000」なので、切り上げても「1」のままです。
但し、小数点以下が表示されていないので、表示形式に「#.0」などを指定して、「1.0」となるようにすべきことが分かります。
一方、⑦を見ると、元の数値が「1.100」に対して、切り上げ後も「1.1」のままですから、きちんと切り上げ処理がされています。
①と⑦の中間の数値である②~⑥についても結果は全て「1.1」となっていて、正常に処理されています。
⑧の「1.101」では、切り上げたた結果が「1.2」となっていて、きちんと意図する結果となっています。
このように、ワードで切り上げ処理を行いたい場合は、
”切り上げる桁に5未満の最大値を加えてからROUND関数を使う”
ことで実現できます。
次に、切り捨ての場合の記述例を示します。
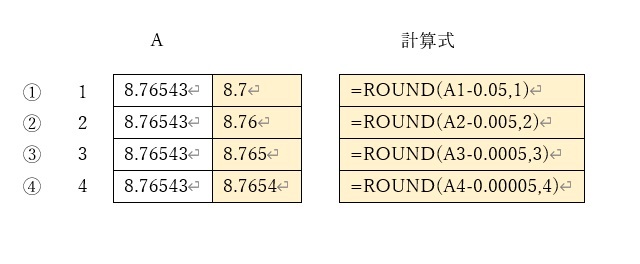
切り捨ても、ROUND関数を工夫して使う
切り捨ての場合も、基本的な考え方は切り上げの場合と同じです。
具体的には、切り捨てる桁から5を引いた後にROUND関数で処理します。
①では、小数点以下二桁を切り捨てて、小数点以下一桁の数字にしています。
処理としては、まるめを行う「A1」から予め「0.05」を引いて、その後ROUND関数でまるめ(四捨五入)ています。
これにより、元の数値「A1」を切り捨てた結果が反映されいることが分かると思います。
切り捨てる桁(小数点以下2桁目)から5を引くことで、ROUND関数による処理が事実上、切り捨てになるのです。
②③④は、まるめる桁数を変えた場合を示していますが、考え方は①と同様です。
いずれも意図する結果になっていることが分かります。
では、切り上げの場合と同様に、もう少し詳しく見てみましょう。
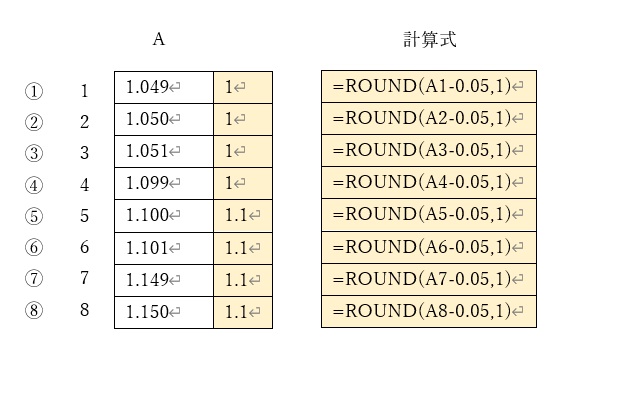
図は全て、小数点以下二桁目を切り捨てています。
処理の境目となる④⑤を見て下さい。
④は、1.1に限りなく近い値ですが、きちんと切り落とされて、1.0になっています。
表示は、「1」になっていますので、切り上げの場合と同様、表示形式で「#.0」と指定して「1.0」と表示されるようにすべきだと言えます。
⑤は、1.1が1.0に切り捨てられることなく、きちんと1.1のままであることが分かります。
①~⑧の全てにおいて、小数点二桁以下がきちんと切り捨てられた結果になっていることが確認できます。
このように、ワードで切り捨て処理を行いたい場合は、
”切り捨てる桁に5を加えてからROUND関数を使う”
ことで実現できます。
なお、小数点以下を全て切り捨てて整数にする場合には、INT関数を利用することもできます。
累乗、指数、平方根(ルート)、立方根、累乗根
エクセルでは、累乗にはPOWER関数が使え、平方根にはSRQT関数が使えますが、ワードではこれらの関数を使えません。
しかし、「^演算子」が利用できますので、累乗や累乗根の計算が可能です。
例を見てみましょう。
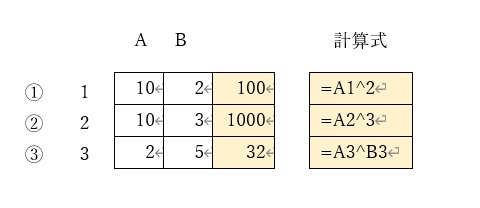
累乗や累乗根には^演算子を使う
①は、10の二乗を計算させた例です。「^演算子」を用いて「=10^2」のように記述すれば、簡単に実現できます。
同様に、②は10の三乗の計算例、③は2の5乗の計算例です。
いずれも、「^演算子」を用いていますが、同様の計算式を記述すれば、ワードでもあらゆる累乗を計算できます。
次は、累乗根についてです。
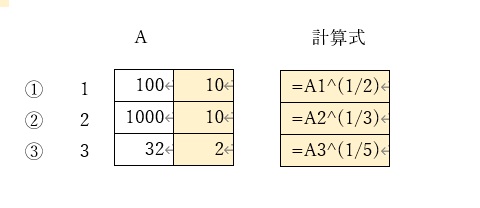
累乗根にも^演算子を使う
分かりやすいように、上記と逆の計算を示しています。
①では、100の平方根を計算させています。
平方根は、1/2(二分の一)乗に相当しますので、100の平方根は、「=100^(1/2)」のように記述すれば実現できます。
「=100^0.5」のように記述しても同じです。
②は、1000の立方根を求めています。
立方根は、1/3(三分の一)乗に相当しますので、1000の立方根は、「=1000^(1/3)」のように記述します。
同様に、五乗根を計算させた例が③です。
五乗根は、1/5(五分の一)乗に相当しますので、32の五乗根は、「=32^(1/5)」と記述できます。
このように、n乗根は、(1/n)乗の計算を行えば実現できますので、どんな累乗根でもワードの表で計算させることができます。
